2D XFEM for Crack eXtended finite element MATLAB code

Mohr-Coulomb plasticity tangential stick-slip rule, penalty method, and Elastic predictor-Plastic corrector algorithm were used. Results are verified with Fushen Liu and Ronaldo I. Borja, “A contact algorithm for frictional crack propagation with the extended finite element method”, INTERNATIONAL JOURNAL FOR NUMERICAL METHODS IN ENGINEERING; arbitrary input geometry, nodal loads, and material properties for each element can be defined by user.

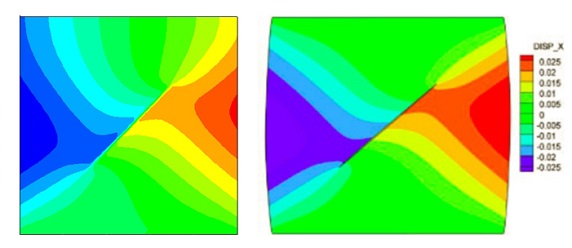
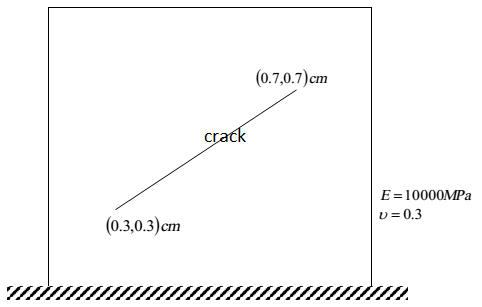
The problem solved in this example is a 1m x 1m rectngle with a crack with length of 0.566m as described below under a -0.1m uniform displacement on the top edge. Find the displacement field (contours) using extended finite element methods using 4-noded isoparametric elements and structured mesh. Use penalty method for the contact.

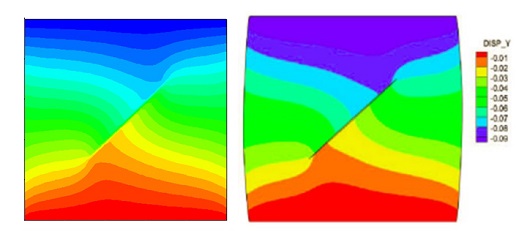
Displacement in y direction is also verified with Borja's paper

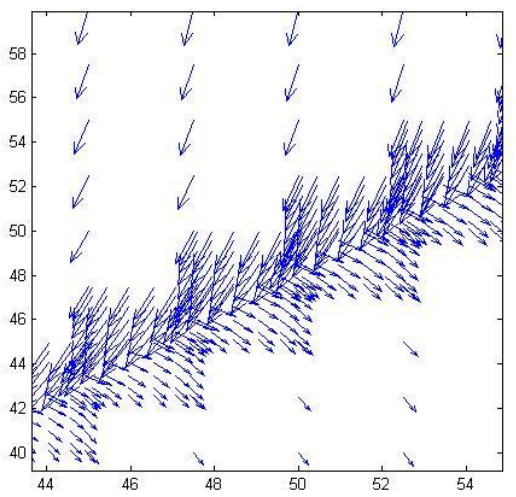
The picture below shows the displacement vectors acting on the crack

What is the eXtended Finite Element Method (XFEM)?

The extended finite element method (XFEM), is a numerical technique based on the generalized finite element method (GFEM) and the partition of unity method (PUM). It extends the classical finite element method (FEM) approach by enriching the solution space for solutions to differential equations with discontinuous functions.
Enriched finite element methods extend, or enrich, the approximation space so that it is able to naturally reproduce the challenging feature associated with the problem of interest: the discontinuity (which is the case in this problem: crack), singularity, boundary layer, etc. Treating problems with discontinuities with eXtended Finite Element Methods suppresses the need to mesh and remesh the discontinuity surfaces, thus alleviating the computational costs and projection errors associated with conventional finite element methods, at the cost of restricting the discontinuities to mesh edges.

eXtended Finite Element Method (X-FEM) Basics

The basic rules of X-FEM are:

discontinuity surfaces are not meshed (they may cut the finite elements),
enrich the elements cut by a discontinuity with new functions through a partition of unity,
usually, although this is not a requirement, the discontinuity is tracked in time and space by the zero iso-contour of a level-set function φ(x; t).

These new functions are chosen a priori by the knowledge of the physical problem at hand. Note that it is not necessary to use a level-set in order to track the discontinuities, but it is convenient for several reasons:

the position of the discontinuity with respect to an element is easily obtained,
the level-set field can be used to define the enriched functions,
the position of the discontinuity can be updated by only updating the level-set function (a scalar field defined on the computational mesh).

Why NOT using the Finite Element Method? - Treatment of free boundary problems: difficulties of the finite element method

”Free boundary problems deal with solving partial differential equations (PDEs) in a domain, a part of whose boundary is unknown in advance; that portion of the boundary is called a free boundary”, writes Avner Friedman. As hinted upon earlier, the Partition of Unity Method, and its siblings (X-FEM, GFEM, enriched meshfree methods) are ideal candidates to efficiently and accurately treat these difficult problems.
Although Finite Element have been popular since the early 1960s in fields ranging from structural and solid mechanics, electromagnetism, fluid and gas dynamics, biological modelling, heat transfer, fluid-structure interaction, buckling analyses, this method in its original design is ill-suited to several classes of problems.

Finite Element Methods approximations are piecewise differentiable polynomial approximations, which are ill-suited to represent problems with discontinuities (either in the unknown field or its gradient), singularities and boundary layers. To accurately model discontinuities with finite element methods, it is necessary to conform the discretization (mesh) to the line or surface of discontinuity. This becomes a major difficulty when treating problems with evolving discontinuities where the mesh must be regenerated at each step. In standard finite element methods, singularities or boundary layers are resolved by requiring significant mesh refinement in the regions where the gradients of the fields are large.

Free moving boundaries occur in a variety of problems of interest to scientists and engineers. Two types of problems excited research on free boundary problems: the ”obstacle problem”, which, in the time dependent case, can be stated as a variational problem, and the Stefan problem describing the process of melting and solidification. More recent free boundary problems include chemical vapor deposition, cancerous tumor growth, coating flows, etc. Solving these problems requires new mathematical treatments which have been subject to active research.

The fractured birth of extended finite element methods

To help remedy the difficulties encountered by finite element methods in solving problems with discontinuities and singularities, partition of unity based, generalized or enriched (extended) finite element methods have been developed. The idea of enriched finite element methods is to extend, or enrich the approximation space so that it is able to naturally reproduce the challenging feature associated with the problem of interest: the discontinuity, singularity, boundary layer, etc. It was shown that such an embedding of the problem’s feature into the approximation space can significantly improve convergence rates and accuracy. Moreover, treating problems with discontinuities with eXtended Finite Element Methods suppresses the need to mesh and remesh the discontinuity surfaces, thus alleviating the computational costs associated with conventional finite element methods. Specially constructed elements that reproduce certain problematic features of a problem have been known for some time. Quarter point elements, for instance have been used effectively to incorporate a stress singularity in crack-tip elements used in computational fracture mechanics. Elements with embedded discontinuities also have been used to model discontinuities in the gradient of the unknown field. However, the effectiveness and ease of implementation of enriched finite element schemes have been significantly improved by the emergence of the Partition of Unity Methods devised by Melenk and Babuska, offering a general scheme to enrich the conventional finite element space with arbitrary functions.

Various forms of the partition of unity method exist: the eXtended Finite Element Method and the Generalized Finite Element Method and enriched meshfree methods. In this course, the implementation of the former method is exemplified. In the first implementation of the X-FEM, a local partition of unity enrichment of standard finite elements was presented to help treat static fracture problems. In this initial work, nodes close to the crack tips were enriched with four functions spanning the near-tip fields of linear elastic fracture mechanics (LEFM). This idea allowed treating cracks independently of the mesh and fracture parameters could be accurately computed with minimal mesh refinement. The nodes whose support is cut by the crack are enriched with a Heaviside function so that the discontinuity of the displacement field across the crack in element interiors could be treated. This work showed the first example of the incorporation of discontinuous functions within the partition of unity framework. A novel method was born allowing to handle arbitrary discontinuities through finite elements. Other examples include quasi-static crack growth, multiple crack propagation in brittle materials, dynamic crack growth, crack growth in Mindlin-Reissner plates, with frictional contact, cohesive crack growth, arbitrary branched and intersecting cracks, bi-material interface cracks, brittle Fracture in Polycrystalline Microstructures. The method later was extended to model inclusions and inhomogeneities using level sets. Recently, Professor Mo ¨ es has been active in geometrically non-linear fracture problems.

Choosing the enrichment

The choice of the enriched functions depends on the a priori solution of the problem. The enrichment is usually given in terms of the level set. Table below shows a few typical enrichments functions for bimaterial, crack, and crack tip.

How can I get this code (matlab files or functions)?

You can have this code for 300 USD. I use PayPal for the sake of buyer's peace of mind because you will be covered by PayPal's purchase protection and you can make sure that you will receive exactly the product described here. When you decided to buy or if you have any questions before the purchase feel free to contact me via email at hosseinali.sut@gmail.com

What other codes are available at matlab-fem.com?

What is Finite Element Method?

The finite element method (FEM) is a numerical method for solving problems of engineering and mathematical physics. It is also referred to as finite element analysis (FEA). Typical problem areas of interest include structural analysis, heat transfer, fluid flow, mass transport, and electromagnetic potential. The analytical solution of these problems generally require the solution to boundary value problems for partial differential equations. Read more about Finite Element Methods

What is MATLAB?

MATLAB (matrix laboratory) is a multi-paradigm numerical computing environment. A proprietary programming language developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages, including C, C++, C#, Java, Fortran and Python.

What reference books did I use for my codes?

Some of the main textbooks I used for codes are:
General concepts and basic codes:

Finite Element Procedures by K.J. Bathe
The Finite Element Method (v.1 & v.2 & v.3) by Zienkiewicz & Taylor
Fundamental finite element analysis and applications by M. Asghar Bhatti

Contact mechanics:

Computational Contact Mechanics by Peter Wriggers

Plasticity:

Finite Elements in Plasticity by D. R. J. Owen, E. Hinton
Non-Linear Finite Element Analysis of Solids and Structures (vol. 1 & 2) by M. A. Crisfield